量子計算如何重塑金融市場 | EntangleTech 量子教育平台

# 量子計算如何重塑金融市場中原大學智慧運算與大數據碩士學位學程助理教授[張晏瑞](https://www.linkedin.com/in/yen-jui-chang-7a5941134/)長年專注於量子計算在優化問題與金融上的應用，尤其是 quantum walk 與 quantum annealing 演算法。張晏瑞老師在上個月熱情接受 EntangleTech 邀請，擔任量子嘉年華的第二場演講講師，為各位介紹量子計算在金融領域上應用的最新發展，接下來我們根據應用的類型，分成金融模擬、資產組合優化、詐欺偵測與程式化交易。 ## 量子演算法簡介在今天的演講，張晏瑞老師主要使用的演算法包括 quantum walk 與量子退火，因此在主題開始之前，我們先簡短介紹這兩個演算法，讓讀者有個初步的概念。 ### Random Walk（隨機行走）在開始介紹 quantum walk 前，我們得先提及它的前身：random walk。想像有個人（walker）在一條線上走路，他會擲出硬幣，若是正面就往右走一步，如果硬幣是背面則往左走一步，重複多次這樣的過程，來統計最後這個人在每個位置上的分佈。

在一維上投硬幣來判斷自己要往左走還是往右走

Picture comes from doi: 10.1007/s11128-012-0432-5

由於每一次都是隨機，這樣的方法可以用於研究許多有隨機成分在裡頭的現象，像是模擬分子在液體裡的運動路徑、動物的搜索路徑，股票價格的波動等等。

硬幣投出正反面的機率剛好是一半（0.5），投擲 100 次後的結果，最後你還在原點的機率是 7.95%，通常 random walk 會呈正態分佈

Picture comes from doi: 10.1007/s11128-012-0432-5

### Quantum Walk（QW, 量子行走）類似的道理，剛剛的貨幣可以改成「量子硬幣」來決定要向左還是向右走，而這「量子硬幣」可以透過 quantum gate 實現各種不同我們想要的機率。與 random walk 不同的是，random walk 的標準差 $\sigma$，與步數 $N$ 的關係是 $\sigma^2\sim T$，而 QW 則為 $\sigma^2\sim T^2$，這意思是 QW 的「擴散」速度比 random walk 還快。

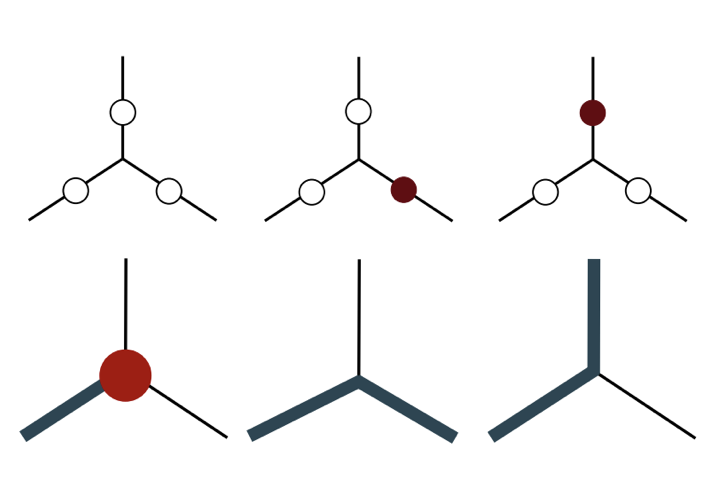
與 random walk 相比，QW 從原點向兩旁的擴散速度更快

Picture comes from arXiv 1001.5326v2

### QUBO 許多優化問題，諸如經典的旅行者問題，都能寫成以下數學形式： \begin{align}\tag{1} \sum_i Q_{ii}x_i+\sum_{j>i} Q_{ij}x_i x_j \end{align} 其中 $x_i$ 是二進位，只能是 $0$ 或 $1$，$Q_{ii}$ 和 $Q_{ij}$ 是個矩陣，攤開來看就是 $x_ix_j$ 的係數，然後電腦要找到一組 $x_i$ 使得（1）算出來的數字最小，這種數學形式我們稱作 quadratic unconstrained binary optimization（QUBO）。

（1）式中的左項理應是 $x_i^2$ 但因為 $x_i$ 只能是 0 或 1，平方還是自己 $x_i$

比方說下式就是一種 QUBO： \begin{align} 3x_0+11x_1+14x_2+19x_3+5x_4 \end{align} 你可以把每個變數 $x_i$ 想成該不該買某個東西，$0$ 就是不買，$1$ 就是買，而每個變數前面的係數 $Q_{ij}$ 就是該物品的價格，而我們希望能夠花越少錢越好。那如果我身上總共只有 3 塊錢

Picture comes from 網路

我希望能剛好把 3 塊錢花完，我們就會加上限制項，即： \begin{align} 3x_0+11x_1+14x_2+19x_3+5x_4+M(3x_0+11x_1+14x_2+19x_3+5x_4-3)^2 \end{align} 其中 $M$ 是懲罰係數，要自己找一個合適的數字給電腦，理應電腦得找到一組解讓上面式子越小越好，很明顯這組解會是 $(1,0,0,0,0)$。凡是這類問題都可以透過 D-Wave 的 quantum annealer（量子退火, QA）求解

D-Wave 的量子退火機

Picture comes from D-Wave

有些公司因為資源不夠豐厚，無法想 IBM 直接大手筆投資量子電腦，但又不想錯過機會，因此 Fujitsu （富士通）利用現代數位電路技術（CMOS）打造專門解 QUBO 的電腦，叫 Digital annealer（數位退火），讓許多公司可以先佈局量子計算但又不用冒大風險投入。

Fujitsu 的量子退火機

Picture comes from 多倫多大學

我們 EntangleTech 正在撰寫 QUBO 的教學，詳細內容可以待我們公布，敬請期待。讓我們回到演講內容 ## 金融模擬量子計算在金融領域中第一個最著名的應用就是金融模擬。在金融市場中，像是股票市場，市場中有很多很多交易者，每個交易者都有自己的一套想法，決定買入或賣出某個股票，而當下股票的價格會是這種多交易者總總決定體現出來的結果，我們能用量子電腦模擬這樣的現象嗎？為此，作者使用 QW 來模擬一個投資者的行為，設計下圖紅框內兩個量子硬幣 $C_{\theta}$ 與 $C_{\theta'}$ 來代表這個投資者選擇買和賣的傾象，當量子硬幣 $C_{\theta}$ 投出來為 $|1\rangle$，代表這個投資者選擇買進，而這動作會使得股價上升（$S+$），反之如果是 $C_{\theta'}$ 投出來是 $|1\rangle$，那價格會下跌（$S-$）。然後把這一個投資者擴增成 $k$ 倍，每個投資者都有自己的買賣清向，最後這種多個 quantum walk 組成的電路如下圖，這電路稱作 multi-split-steps QW (multi-SSQW)，最後加上一個古典的 optimizer 形成一個類似 variational quantum algorithm，根據計算結果與真實資料的差異會去調整每個參數 $C_{\theta}, C_{\theta'}$。

multi-SSQW 電路圖

接著作者使用 2022 年 1 月至 3 月每日 J&J （一家美國藥廠）、Apple、Microsoft、S&P 500 與 NASDAQ 100 股票資料作為訓練集，根據每次 QW 跑出的機率分佈與真實資料的差異來回調整參數

（左圖）真實 S&P 500 的歷史資料（trained）以及 multi-SSQW 擬和結果（target）；（右圖）multi-SSQW 模擬過程的收斂結果

根據模擬結果，整體看起來擬和得非常好，尤其是 S&P 500 與 NASDAQ 100，且展現快速又穩定的收斂結果，使這方法可以成為金融分析與模擬的有力工具。 ## 資產組合優化當你想要投資的金融商品很多時，比方說你想投資 VTI, VXUS, 與 BNDW，你該如何分配各商品的投資比例，以達到最高獲利與最低風險，這就是美國經濟學家 Harry Markowitz 在博士期間嘗試解決的問題，他的博士論文促成現代投資組合理論（MPT）發展，在他的[博士論文](https://www.math.hkust.edu.hk/~maykwok/courses/ma362/07F/markowitz_JF.pdf)中，他提出[效率前緣](https://kopu.chat/mutual-fund-theorem/)（Efficient Frontier）的概念。當我們把各種商品的投資組合，根據其預期報酬率（return）、風險（標準差）與比例做計算後，可以畫成下圖，而獲利最高且風險最低的資產組合位於紅色線上，這條線稱作 efficient frontier。

將不同資產不同比例組合的獲利與風險畫成圖，最佳組合落在紅色線上

Picture comes from moneytothemasses

當今天想投資的標地越來越多時，組合越來越複雜，計算量會隨之劇增，對現在的電腦來說也是一種負擔，那我們能不能借助量子計算減輕計算負擔呢？這也是作者今天想回答的問題。為此，作者寫出這樣的公式： \begin{align}\tag{2} H=\theta\cdot \bigg(\sum_{i=1}^n\sum_{j=1}^n \mathrm{cov}(i,j)\cdot x_ix_j\bigg)-M\cdot(\sum_{i=1}^n x_ir_i-R)^2 \end{align} 上述這公式從左至右分別代表資產組合的風險與報酬，其中 $x_i$ 代表第 $i$ 個商品所佔比例， $r_i$ 是商品 $i$ 的預期報酬率，$R$ 是我們能接受的最低報酬率，$M$ 是懲罰係數，所以右項代表要盡可能找到預期報酬高於 $R$ 的組合，左項 $\mathrm{cov}$ 代表這兩個商品 $i,j$ 之間的 covariance，$\theta$ 也是個我們自己定義的係數，這項代表要盡可能找到風險小的組合。由於 QUBO 的變數只能是 $0$ 和 $1$，作者得找個方法將比例（$0\sim 1$）轉成 $0$ 和 $1$，因此定義： \begin{align}\tag{3} x_i\approx \sum^K_{k=1} \frac{1}{2^K}\cdot 2^{k-1}\cdot x_{i,k} \end{align} $K$ 代表要多精確地表達 $x_i$ 這個比例。將上式代入（2）式得到 QUBO 形式： \begin{align}\tag{4} H=\theta\cdot\sum_{i=1}^n\sum_{j=1}^n \mathrm{cov}(i,j) \bigg(\sum_{k=1}^K \frac{1}{2^K} 2^{k-1} x_{i,k}\bigg)^2 -M\cdot\bigg[\bigg(\sum^n_{i=1}(\sum_{k=1}^K \frac{1}{2^K} 2^{k-1} x_{i,k})\cdot r_i\bigg) -R\bigg]^2 \end{align} 在論文中，作者使用 S&P 500 中 40 支股票真實數據，利用 Monte Carlo simulation 尋找合適的超參數 $\theta, M, K$，然後利用數位退火求解。比方說當 $K$ 越大，QUBO 中的變數越能精確表達每個資產所佔的比例，計算出的結果越能接近實際的 efficient frontier。

藍線代表真實的效率前緣，不同的 K 值計算出的結果，K 越大越能接近實際結果

在論文中，作者也提出 two-stage search，來避免模型陷入局部最低點出不來，詳情可以參考文末參考文獻。 ## 詐欺偵測

對於銀行，最重要的是如何抓出可能是洗錢的帳戶，那最常的做法就是利用大數據給機器學習訓練，找出可以判別有疑慮帳戶的特徵（features），像是小金額多次轉帳，為此，我們會先把大量帳戶資料整理成下列這樣的矩陣： \begin{align} D= \begin{bmatrix} D_{11} & D_{12} & \cdots & D_{1n} \\ D_{21} & D_{22} & \cdots & D_{2n} \\ \vdots & \vdots & \vdots & \vdots & \\ D_{m1} & D_{m2} & \cdots & D_{mn} \end{bmatrix} \end{align} 每一個 column 都是 features，像是帳戶名字、存款金額、交易紀錄、交易時間等等，而每一個 row 就代表一個帳戶。以這個矩陣為例，總共有 $n$ 個 features，$m$ 的帳戶。然後我們會有個已知的答案，哪些帳戶是洗錢帳戶，哪些是像筆者這樣的正常窮人帳戶，也整理成矩陣 $O$： \begin{align} O= \begin{bmatrix} O_1 \\ O_2 \\ \vdots \\ O_m \end{bmatrix} \end{align} 接著將這兩個矩陣丟進機器學習模型，尋找主要 features。然而，當 features 非常大量時，計算時間會隨之劇增，因此作者也想知道，是否能借助量子計算加快計算速度，更快從矩陣 $D$ 中找到主要特徵。首先，一樣要先設計一個 QUBO： \begin{align} f(x)=-\alpha \sum^n_{j=1}x_j |\rho_{oj}|+(1-\alpha)\sum_{j=1}^n\sum_{k=1,k\neq j}^n x_jx_k |\rho_{jk}| \end{align} 其中 $x_j$ 代表要不要選特徵 $j$，$\alpha$ 是 influence term，$\rho_{oj}$ 代表特徵 $j$ 與結果 $o$ 的相關係數，$\rho_{jk}$ 就是特徵 $i$ 與 $j$ 的相關係數。由於不容易取得銀行資料，作者使用比特幣的公開資料做訓練，總共有 694,676 個 addresses 以及 3,459,773 個交易紀錄，然後分成三組做計算，分別是單純機器學習從 $D$ 中找到主要特徵、先用模擬退火（SA）找到主要特徵再交給機器學習做訓練，以及先用 D-Wave QA 找到主要特徵再交給機器學習做訓練。如果今天單純使用古典機器學習，能從矩陣 $D$ 找到 69 個主要特徵，使用 SA 則能將特徵數降到 23 個，QA 則 9 個：

不同演算法抓出的主要特徵數量

計算表現與訓練時間如下。在古典機器學習中（Logistic 到 Neural network），以 random forest 的表現最好，精準度（accuracy）高達 95%，但訓練時間將近 5 個小時；然而在 SA-random forest 中，特徵數從 69 掉到只剩 23 個，accuracy 僅下降 1%，但訓練時間縮短了三分之一，大大降低計算時間。

## 程式化交易另一種量子計算可能的應用是程式化交易，像是外匯套利。假設有兩家銀行 A 與 B，但在某個時間點，兩家銀行接受到資訊的速度不一樣，使得兩家銀行對美金與歐元的定價不同： - A 銀行的買入 1 歐元的價格 1.61 美金，賣出價格 1.62 美金 - B 銀行的買入 1 歐元的價格 1.63 美金，賣出價格 1.64 美金你可以向 A 銀行買入歐元（花了 1.62 美金），然後向 B 銀行賣出歐元（得到 1.63 美金），從中獲利 0.01 美金。以上是簡單的外匯套利範例，然而實際市場上的資產（貨幣）非常非常多，每個貨幣之間的匯率也不斷在變動，電腦必須在極快的速度算出最好的策略，推薦投資者可以怎麼換貨幣以得得最高獲利，目前比較常用的演算法有 Bellman-Ford's 演算法與 Floyd-Warshall's 演算法，兩者演算法[複雜度](https://www.entangletech.tw/lesson/basic-algorithm-05)分別是 $O(|V||E|)$ 與 $O(|V|^3)$（$|V|$ 是貨幣數量，$|E|$ 是每個貨幣之間匯率的總數量）。

有這麼多的貨幣與匯率，交易者要能在其中找到一條迴路（藍色線），將日幣換成各種貨幣，最後換回日幣還能獲利

Picture comes from 1QBit

那換成量子電腦能做得更快更好嗎？1QBit 在白皮書中提供了他們的做法，一樣先得把問題轉成 QUBO 形式： \begin{align} x=\mathrm{argmax_x} \bigg[ \sum_{(i,j)\in E} x_{ij} \log{c_ij} -M_1 \sum_{i\in V}\bigg(\sum_{j,(i,j)\in E}x_{ij}-\sum_{j,(j,i)\in E} x_{ji} \bigg)^2- M_2 \sum_{i\in V}\sum_{j, (i,j)\in E}x_{ij}(\sum_{j, (i,j)\in E}x_{ij}-1)\bigg] \end{align} 然後一樣透過 QA 或是數位退火找到可以獲利的迴路。不過講者認為在市場極高效率的今天，套利空間越來越小，套利空間稍縱即逝，為了在幾微秒內抓住這機會，投資者除了要把運算資源直接放在交易所旁邊，甚至交易所裡面，把運算資源寫成 FPGA 晶片外，還得解決如何更快地解密封包（銀行的貨幣資料進來）與送出封包（做出買賣決定），因此講者認為或許量子電腦在這方面能做的加速很有限。

本文章僅提供演講摘要，詳細內容可以看完整影片

## 參考文獻與延伸閱讀 - [完整演講影片](https://www.youtube.com/watch?v=5hFSWdS89lk) - [A novel approach for quantum financial simulation and quantum state preparation](https://arxiv.org/abs/2308.01844) - [Quantum-Inspired Portfolio Optimization In The QUBO Framework](https://arxiv.org/abs/2410.05932) - [Efficient Bitcoin Address Classification Using Quantum-Inspired Feature Selection](https://www.arxiv.org/abs/2411.15425) - [Finding optimal arbitrage opportunities using a quantum annealer](https://1qbit.com/files/white-papers/1QBit-White-Paper-%E2%80%93-Finding-Optimal-Arbitrage-Opportunities-Using-a-Quantum-Annealer.pdf)