量子模擬 String Breaking 現象 | EntangleTech 量子教育平台

# 量子模擬 String Breaking 現象中性原子量子電腦公司 QuEra 與幾個頂尖大學合作，使用該公司的中性原子量子電腦（Neutral Atom Quantum Computer）模擬量子色動力學（QCD，描述夸克、膠子之間強交互作用的理論）裡的 string breaking現象，並將研究結果發表在《Nature》上。 ## 前情提要 ### 夸克禁閉你可能在科普裡聽過這名詞，或說現象，你無法觀察到「單獨」的夸克（quark）。夸克之間透過強核力（strong interaction）綁在一起，強核力相比其他基本力有個很特別的性質，距離越遠，力越大，其他基本力都是距離越遠，力越小。

大部分的基本力（紅色的重力、藍色的電磁力與綠色的弱核力均隨著距離越遠，強度越弱，但強核力（紫色）反而是增加

Picture comes from doi: 10.1088/0264-9381/32/3/033001

當你想把兩個（或三個）綁在一起的夸克分開，夸克之間的距離越遠，強核力的力道越大，最後會像圖下一樣，能量大到可以產生一對新粒子（質能轉換），這也是為何我們無法觀察到單獨的夸克，他就像磁鐵一樣，你怎麼分開，他就是要成對存在（應該是說，[color](https://zh.wikipedia.org/zh-tw/%E8%89%B2%E8%8D%B7) = 0，這邊的 color 也不是真的顏色，而是一種類似你在化學裡學過的一種量子數，而這量子數的出現是因為對稱性）。

string breaking 示意圖

Picture comes from Wiki

如上圖所示，若我們將一對夸克強行拉開，中間連接 quarks 的通量管（flux tube）會變得像一條「**弦（String）**」，而這個「**弦斷掉並產生新粒子對**」的現象，即稱作「**String Breaking**」，本研究正是想透過原子系統的建構，模擬該現象的機制。 ### Rydberg 原子與量子電腦當一個原子的一個電子被激發到很遠很遠的地方，這種原子就稱作「Rydberg atom」，或說這原子達到 Rydberg state $|r\rangle$，而這位居很遠的電子讓 Rydberg atom 具備許多特性： 1. 原子半徑很大，以氫原子為例，當電子被激發到 $n=137$，其半徑可以到將近 1 微米 2. 由於這顆電子距離原子核非常遠，像是在世外桃源，因此其壽命很長，以 $Rb$ 原子為例，位在 $50s$ 軌域的電子壽命長達 126 微秒（作為比較，位在 $5p$ 的電子壽命僅有 0.0206 微秒。 3. 上述的世外桃源是相比於內層的電子，由於太外面了，也代表其很容易受到環境干擾除此之外，因為距離太遠，這電子與原子核形成很大的 dipole，這 dipole 會改變鄰近原子的能階，使得鄰近原子無法達到 Rydberg state，這現象稱作 "Rydberg blockade"。

左圖是不同狀態的兩個原子（由下而上分別是兩個都處於基態、其中一個達到 Rydberg 態，以及兩個原子都達到 Rydberg 態）的能量與距離的關係，可以發現隨著原子間的距離越近，要同時出現兩個 Rydberg atom 所需的能量是劇增；右圖展示一個 Rydberg 原子附近一段距離內的原子都無法達到 Rydberg state

Picture comes from doi: 10.1088/1674-1056/abd76f

Rydberg atom 的第三點特性使得其可以作為量子感測，感測環境的變化，而 blockade 的性質則讓 Rydberg atom 容易做 quantum gate 操作，使其成為實現量子計算的其中一種方式，即中性原子量子電腦，也是 QuEra 這家公司在專研的領域。 ## 模擬 String Breaking 由於直接用原子系統模擬 quark 的性質過於艱難與複雜，因此團隊先簡化問題，將問題簡化成兩個電荷，中間有電磁力互相吸引，但這電磁力與你生活中熟悉的電磁力不同，這電磁力的強度會隨著兩個電荷之間的距離越大而增大，如下圖所示，這就是今天 QuEra 要模擬的系統：

兩個電荷，類比成夸克，之間會有一股無形的力量牽制著他們，這力量隨著距離越遠會越大，當大到一個程度後會斷掉，生成一對（兩個）新電荷

接著團隊透過公式推導，找出原子系統與欲模擬系統之間的對應關係，如下圖所示，要模擬一個正電荷與 string 需要準備三個原子且都位於基態（上欄，從左往右數第二張圖）

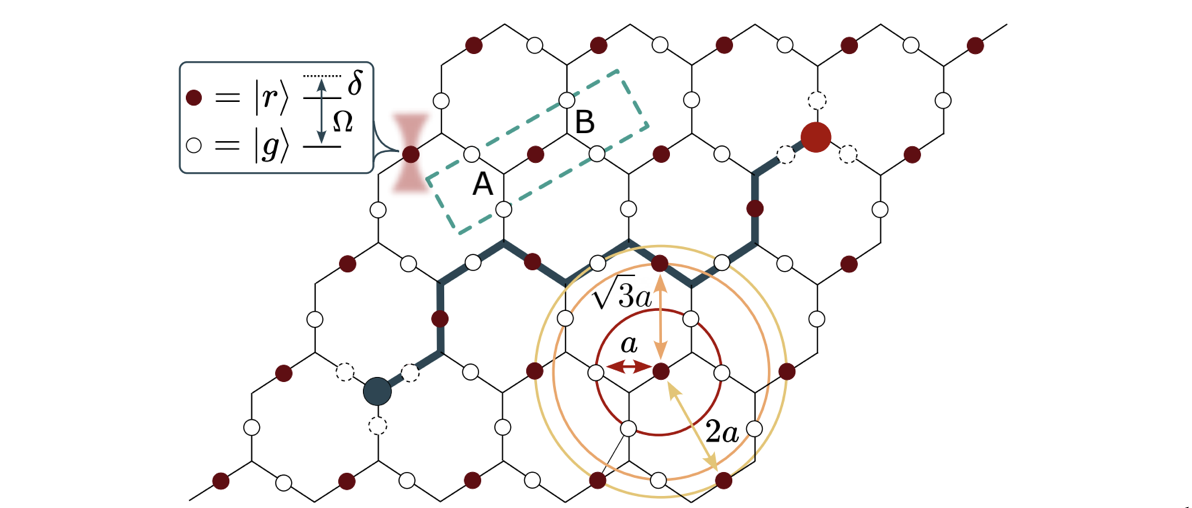
原子系統與欲模擬系統之間的對應關係。白色圈圈是處於基態的原子，紅色小圈圈是 Rydberg 原子；藍色圈圈是正電荷，紅色大圈圈是負電荷，藍色粗線是 string

比方說要模擬 string 斷掉後產生兩個新電荷，對應到原子系統就是簡單地用雷射把處於 Rydberg state 的原子躍遷回基態，如下所示

左圖是原子系統，右圖是欲模擬的系統

最後會像下圖這樣，背景是 Rydberg 原子陣列，以及其對應欲模擬的系統：

左上小匡代表 g 基態與 r Rydberg 態對應的能階，以及兩個代號代表的意思，右下角在表達 Rydberg blockade

根據團隊的公式推演，他們使用雷射參數 $\frac{\delta}{\Omega}$ 比擬電荷的質量，Rydberg atom 的勢力範圍 $R_b$ 比擬為 string 的張力，畫出了這張圖：

string 斷掉的機率隨著電荷質量與 string 張力的變化

橫軸是電荷質量，縱軸是 string 的張力，顏色代表 string 不斷掉的機率減去斷掉的機率，可以發現當電荷質量越大，string 越不容易斷掉（圖中標示的 "String"），當 string 的張力越強，這股能量越容易大到會斷掉並產生新粒子（圖中標示的 "Broken string"）。 ## 實驗結果團隊設定了兩個電荷，而這兩個電荷之間的 string 可以有各種不同但長度相同的構型，如下圖所示的構型 1~6，但 string 斷掉並產生一對新電荷，就是構型 0

構型 0 是斷掉了，構型 1~6 是相同長度不同構型的 string

接著固定質量，並觀察不同 string 張力下的構型分佈，如下圖所示。當張力比較弱時（e 與 g），string 不容易斷掉，因此出現構型 0 的機率幾乎沒有，而最容易出現的構型是 1 和 6；當張力比較強時（f 與 h），string 容易斷掉，因此構型 0 的出現機率最高，其他都近趨於 0。

質量固定，不同張力的 string 下，構型的理論與實驗機率分佈

接著團隊先觀看 string 斷掉的"動態"過程，模擬的方式如下圖所示。原本的構型處於 s，當兩個電荷距離越拉越遠，string 強度越來越大，最後斷掉，但斷掉會有不同斷掉的方式，可能會斷成構型 b，或者是產生的一對新電荷的 string 也斷掉，變成構型 c：

箭頭不代表演化順序，只是對該構型打一道雷射後會變成哪個系統

然而在這次的系統中，無法在計算過程中，直接移動電荷（或是說原子）到遠處，這也是為何上圖兩個電荷之間的距離根本沒變，因此必須透過另一種方式來比擬因為距離增大，力的強度越大這種現象，那在原子系統中，也可以透過雷射參數 $\frac{\delta_0}{\Omega}$ 來類比。當 $\frac{\delta_0}{\Omega}=0$ 時（下圖的 c），代表距離還沒拉開，因此出現機率最高的當然是構型 s；當距離漸漸拉開，構型 s 的出現機率隨時間大減，構型 b 增加，如果距離繼續拉開（$=3$）時，新產生的 string 再斷掉變成構型 c。

## 參考文獻與延伸閱讀 - [論文連結](https://www.nature.com/articles/s41586-025-09051-6) - [中性原子量子電腦簡介](https://www.youtube.com/watch?v=z280osP2SFI&t=4060s)