迄今為止量子電腦模擬最大的蛋白質 | EntangleTech 量子教育平台

# 迄今為止量子電腦模擬最大的蛋白質這篇論文是由離子阱量子電腦領導廠商之一 IonQ 與 Kipu Quantum 合作發表，在 IonQ 的量子電腦上使用 Kipu Quantum 此前發表的 BF-DCQO （bias-field digitized counterdiabatic quantum optimization）演算法模擬蛋白質結構模擬、MAX 4-SAT 和 all-to-all spin glass 問題上，研究結果目前預刊在 arXiv 上，本文章將重點著重於蛋白質模擬的部分，在這篇論文中，使用了 33 個 qubits 模擬了 12 個氨基酸長的蛋白質結構，為迄今為止量子電腦模擬最大的蛋白質。 ## QUBO 與量子退火我們在[新聞文章](https://www.entangletech.tw/post/liang-zi-ji-suan-ru-he-chong-su-jin-rong-shi-chang)裡提過 QUBO 的概念，把問題寫成 QUBO 形式後就能透過量子退火尋找問題的最優解（但不一定是最佳解）。在量子退火中，qubits 的安排入下圖所示：

2D Ising model
Picture come from Wiki

目前關於 QUBO, 量子退火與 QAOA 演算法的教學文章仍在草稿階段

圖中每一個箭頭都是一個 qubit，箭頭向上向下代表 qubit 處於的狀態（$|0\rangle$ 或 $|1\rangle$），我們可以輕易地透過外加此場改變所有 qubits 的狀態，而量子退火便是透過這樣的原理尋找最優解。一開始先設定後每個 qubit 的初始態，當下這系統的能量，我們記做 $H_i$，而我們欲求某個 QUBO 的問題記做 $H_p$，接著透過外加磁場慢慢地把系統能量從 $H_i$ 改變到 $H_p$，而外加磁場的改變會影響到每個 qubit 的狀態，這段過程每個 qubit 的變化會像下圖最下方的藍線一樣，從最左邊沿著藍線演化到右邊，之所以要「緩慢」變化是因為我們要求能量最小的組合，如果演化太快，系統可能會越躍遷到激發態，那就不是能量最低的組合，到了最右邊後，當下每個 qubit 的狀態就是能量最低的組合，在蛋白質模擬中，可能就對應每個氨基酸的位置。

退火示意圖
Picture come from D-Wave

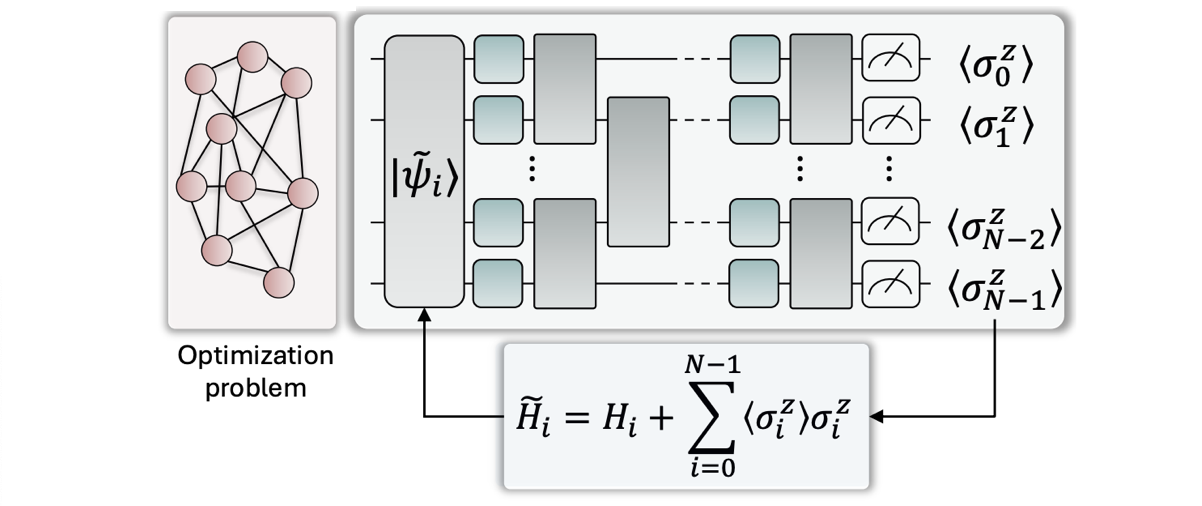
上述這過程可以透過下面簡單的方程式做描述，$\lambda$ 是一個與時間 $t$ 有關的函數，我們稱作排程（schedule）。當 $t=0$ 時 $\lambda=0$， $H_{ad}=H_i$，當 $t=T$ 時，$\lambda=1$，$H_{ad}=H_p$。 \begin{align}\tag{1} H_{ad}=(1-\lambda)H_i+\lambda H_p \end{align} ## BF-DCQO 演算法量子退火雖然已經應用在很多優化問題上，然而其致命的問題是要「緩慢」演化，然而量子電腦都有計算時間限制（coherence time），拖越久錯誤率越高，要如何加速演化速度又不用擔心系統跳到激發態，為此科學家提出 "counterdiabatic" 概念，即在（1）式上添加一個抵銷項，即： \begin{align}\tag{2} H_{cd}=H_{ad}(\lambda)+\frac{d \lambda}{dt}A_{\lambda} \end{align}

抵銷項的來由就是計算系統跳到激發態的機率，然後把它扣掉，實務上也是透過外加磁場實現（在量子退火裡）

不過 IonQ 不是做量子退火，所以得把量子退火的過程分解成一個一個 quantum gate 來擬似量子退火，經過分解後，（1）式中的 $H_i$ 對應到下圖紫色方塊，[$R_y$](https://www.entangletech.tw/lesson/basic-algorithm-10#toc-7) gate，剩下的部分對應到下圖大括號中的 gate（包括綠色與灰色方塊）並重複 $n$ 遍，取決於你希望答案算得多精準。

BF-DCQO 演算法量子電路示意圖

接著會透過每次電路運算出的結果經過一些代數運算後，與這次的初始態 $H_i$ 加在一起變成下一次運算的初始態 $\widetilde{H}_i$，根據新的初始態更新上圖紫色方塊的角度，再做一次計算，如此循環，理論上越多次循環越接近最優解，整個演算法的過程可以用下面這張圖表示：

BF-DCQO 演算法示意圖

上圖中敘述這種初始態更新方法的意思是，上一次測量 qubit 的結果，如果該 qubit 的量子態很接近 1，那再下一次計算時就讓該 qubit 的量子態設定得更接近 1（機率上更接近 1），中括號刮起來的部分，作者定義了兩種方法，詳情可以看參考文獻第二篇

另外，如果對應出來的 gate 角度太小，對整體的計算影響不大，為了節省硬體資源可以將這 gate 省去，在論文中作者會設定一個閾值，小於這閾值的 gate 就刪掉，閾值越大代表刪掉的 gate 越多，視不同問題，作者會設定兩個閾值，閾值比較大的稱作 "hard"，反之比較小的稱作 "soft"。 ## 蛋白質模擬在簡單地介紹過以上兩個論文中提及的概念，現在我們把話題拉回蛋白質的模擬。首先，蛋白質的折疊本質上是一種搜尋能量最低的問題，這種問題通常需要在巨大的空間裡找到最佳或是接近最佳的解決方案，在蛋白質的摺疊中，尋找的就是在晶格上最低能量的空間（相對）位置。蛋白質摺疊建模之優化問題通常涉及在二維或三維晶格上搜尋最低能量構象。這可以重構為量子基態問題。論文中採用的蛋白質建構方法為：將氨基酸排列在四面體晶格（tetrahedral lattice）中，將蛋白質的第一個氨基酸放置於晶格中某個位置，接著就像貪吃蛇遊戲，下一個氨基酸就把它放在上、下、左、右四個方向之一的鄰近格子裡，方向用 2 個 qubit 來表示，因為 2 qubit 可以表達 4 種狀態（$00、01、10、11$），這種編法方式稱作 dense encoding

蛋白質模擬的四面體晶格
Picture comes from doi: 10.1038/s41534-021-00368-4

而蛋白質摺疊時會有能量上的考量，有些氨基酸靠近時會互相吸引或排斥，像是親水性氨基酸傾向與親水性氨基酸靠在一起，能量會降低，而與疏水性氨基酸靠在一起時，能量會升高。在這篇論文裡，作者使用的是一種簡化的能量模型 Miyazawa–Jernigan contact energy，它只考慮那些在晶格上相鄰但在鏈上不相連的氨基酸對，這些就叫做「最近鄰接觸」，將其轉為 Hamiltonian，即論文中的（8）式。論文中他們一共模擬了三種蛋白質，Chignolin、Head activator neuropeptide 與 immunoglobulin kappa joining 1 gene segment，結果如下圖，橫軸代表不同能量值對應的蛋白質構型，縱軸代表該能量下蛋白質可能的構型種數，就不是結構不同能量就不同，常常很多是結構不同卻對應一樣的能量，也因此即便量子電腦算出來的能量值與經典算法一樣，也不太表他們倆預測的蛋白質構型長得一樣。

三角形標記為執行 BF-DCQO 演算法 10 次迭代後獲得的最低能量值，有 soft 與 hard 的結果，其中 PP 代表如果他們覺得量子電腦計算出的結果不滿意，就再用模擬退火做修正。星星標記是經典電腦算出來的結果（brute force method）。對於蛋白質模擬，BF-DCQO 搭配 PP 在這三種氨基酸序列中都能預測到與經典算法類似的能量值，與經典電腦計算相比，誤差在$10^{−1}$ 到 1 之間，聽起來不樂觀，但能從幾乎有 $10^5$ 種可能的構型中優化到如此小的誤差，而且構型類似，已經很厲害了。

實驗結果

在上圖這表格中，展示了用到幾個 Pauli terms（$n_{terms}$），以及在這十次 iterations 中使用到最少與最多的 two qubit gate（ZZ gates）數量，量子電腦計算出最好的結果（Best solution），加上 PP 後最後的結果（Best solution (PP)）以及經典方法的結果（Optimal solution），可以發現 BF-DCQO+PP 計算出的能量值與經典方法幾乎一樣。 ## 參考資料 1. [最早有關 BF-DCQO 的論文](https://arxiv.org/pdf/2405.13898) 2. [BF-DCQO 用於 HUBO 問題](https://arxiv.org/pdf/2409.04477) 3. [本篇論文連結](https://arxiv.org/pdf/2506.07866)