半加法器的電路圖
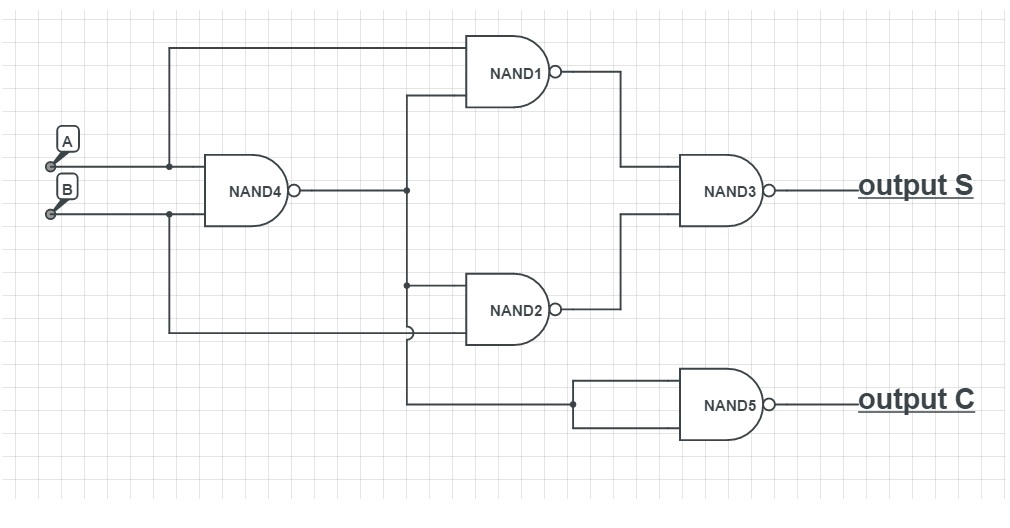
半加法器的電路圖
## Reversible gates(可逆邏輯閘) Reversible gate 是指能單靠 gate 的輸出值就能判斷原本的輸入是什麼,比方說 NOT gate:在量子電腦上也是,有許多不同的量子邏輯閘供我們使用,但硬體層面不一定支援所有的 gate。因此,一台好的量子電腦至少得能做 universal gate 操作,才能用這些基本的 gate 組合出其他種 quantum gate。
NOT gate 的電路圖
AND gate 的電路圖
那該如何解決 AND gate 的不可逆性導致的能量浪費呢?這時候就得用一個特別的邏輯閘叫 Toffoli gate(or CCNOT gate),它是一個可逆版的 AND gate這邊指的是理論上,實際上會更複雜
Toffoli gate 的電路圖
CNOT gate 的電路圖
在量子電腦中,所有的 quantum gate 都是可逆,因此量子電腦可以在沒有能量消耗的情況下做計算
這節我們介紹了通用邏輯閘集合和可逆邏輯閘的概念,這些概念對理解量子計算非常重要。在進到量子計算前,我們還得先介紹何謂演算法複雜度。到介紹量子邏輯閘的時候,會再遇到 CNOT 與 Toffoli gate




